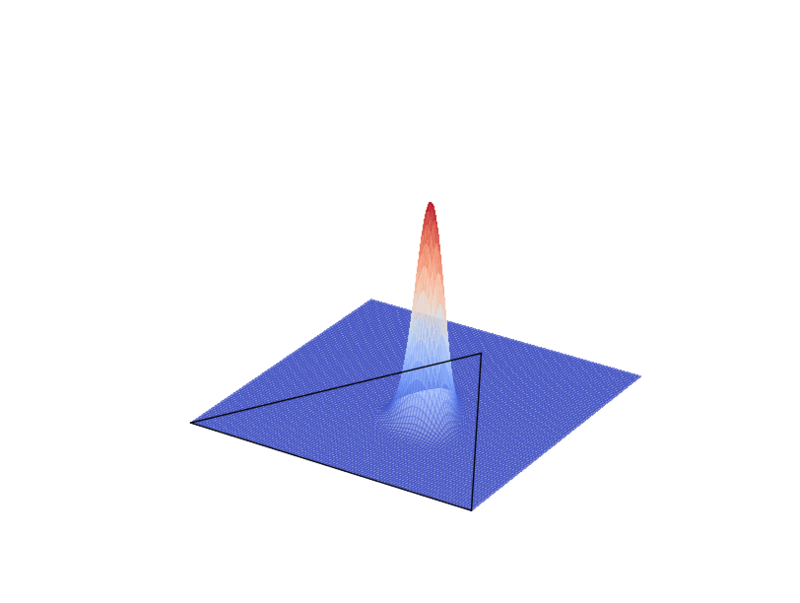
ディリクレ分布を立体的に表示する

ディリクレ分布をRとpythonで描いてみるの続き。今回はRで書くのがしんどかったのでpythonのみ。

from __future__ import division
from scipy.special import gammaln
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import  matplotlib.patches as patches
from matplotlib.path import Path

# ディリクレ分布確率密度
def dirichlet_pdf(xs, alphas):
    xs, alphas = np.array(xs), np.array(alphas)
    if np.any(xs < 0) or np.any(xs > 1):
        return 0
    else:
        ibeta = np.exp(gammaln(alphas.sum()) - gammaln(alphas).sum())
        return ibeta * (xs ** (alphas - 1)).prod()

fig = plt.figure()
ax = fig.gca(projection = '3d')

# ディリクレ分布
X = np.arange(0, 1.01, 0.01)
Y = np.arange(0, 1.01, 0.01)
X, Y = np.meshgrid(X, Y)
x1 = 1 - X - 3**(1/2) * Y / 3
x2 = X - 3**(1/2) * Y / 3
x3 = 2 * 3**(1/2) * Y / 3
Z = np.array(
    [[dirichlet_pdf((x1[i, j], x2[i, j], x3[i, j]), (11, 21, 31))
        for i in range(101)]
        for j in range(101)]
    )
# プロットの軸がなぜかずれるのでXとYの順番を入れ替えた
surf = ax.plot_surface(Y, X, Z, rstride=1, cstride=1, cmap=mpl.cm.coolwarm,
        linewidth=0, antialiased=False, alpha=0.6)

# 正三角形
verts = [(0, 0, 0), (1, 0, 0), (0.5, 3**(1/2)/2, 0), (0, 0, 0)]
for i in range(3):
    x = verts[i][0] + (verts[i+1][0] - verts[i][0]) * np.arange(0, 1.01, 0.01)
    y = verts[i][1] + (verts[i+1][1] - verts[i][1]) * np.arange(0, 1.01, 0.01)
    z = verts[i][2] + (verts[i+1][2] - verts[i][2]) * np.arange(0, 1.01, 0.01)
    ax.plot(x, y, z, color="black", linewidth=1)

# 軸を表示しない
ax.set_axis_off()

plt.show()