2項分布、ベータ分布をRとpythonで描いてみる

2項分布

• R $$ P(X=k) = \begin{pmatrix} n\\ k\\ \end{pmatrix} p^{k}(1-p)^{n-k} $$

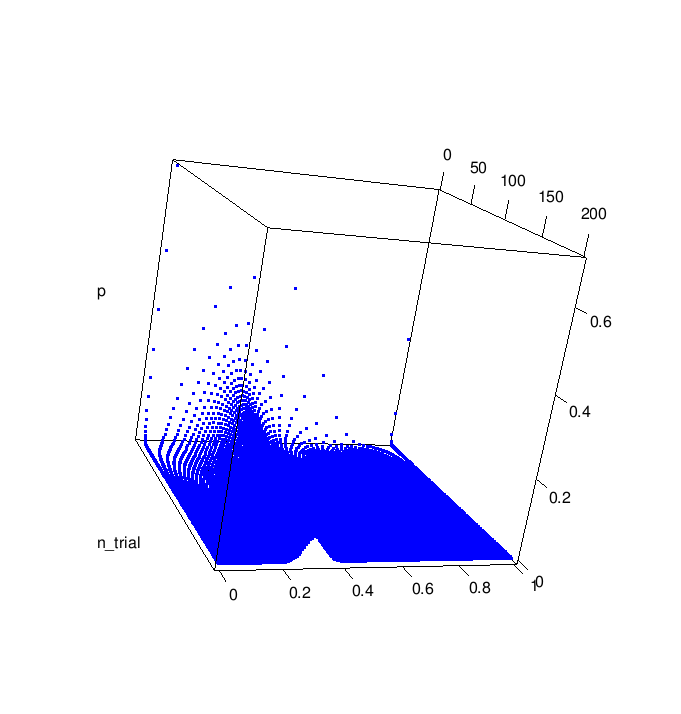
library("rgl")

#サイコロを投げる最大の回数
N <- 200
#成功率
p <- 0.3

#投げる回数をx、成功する割合をy、その場合の確率をzとする
x <- y <- z <- rep(0, 1/2*(N+1)*(N+2)-1)
head <- 1
for (n in 1:N){
  x[head:(head+n)] <- n
  y[head:(head+n)] <- (0:n) / n
  z[head:(head+n)] <- dbinom(0:n, n, p)
  head <- head + n + 1
}

plot3d(x, y, z, pch=20, col="blue", xlab="n_trial", ylab="success_rate", zlab="p")
rgl.snapshot("binom.png")

Nが大きくなるとそれぞれの仮説ごとの確率は小さくなるが0.3付近に収束して行っているのが分かる。

• python

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolskits.mplot3d import Axes3D
from scipy.stats import binom

N = 200
p = 0.3

x = np.hstack([[n]*(n+1) for n in range(1, N)])
y = np.hstack([np.arange(n+1)/n for n in range(1, N)])
z = np.hstack([binom.pmf(np.arange(n+1), n, p) for n in range(1, N)])

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c="blue", marker=".", linewidrh="0")
ax.set_xlabel('n_trial')
ax.set_ylabel('success')
ax.set_zlabel('p')

plt.show()

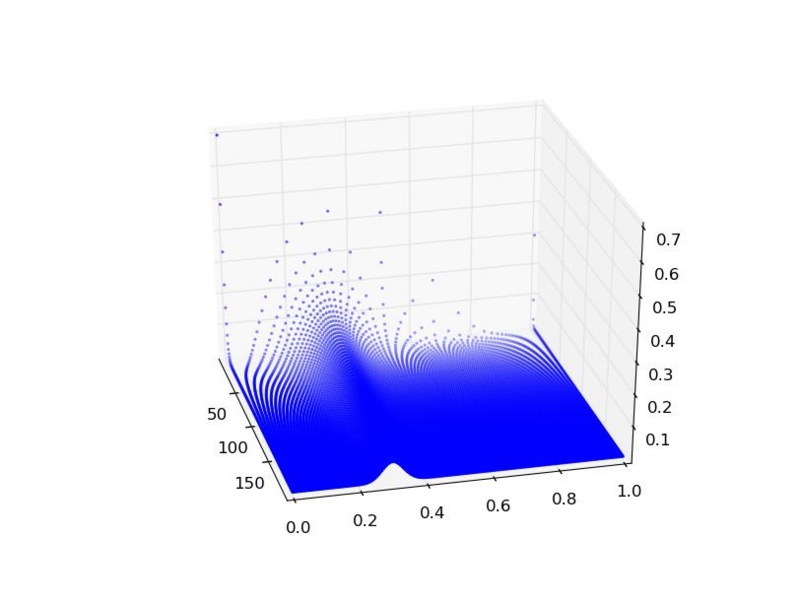
軸のラベルの設定忘れれたorz

ベータ分布

例えばサイコロを振って$m $回、$n$回表と裏が出た時、 $\alpha = m+1, \beta = n+1$として、

$$ p(x, \alpha, \beta) = \dfrac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta-1} $$ $$ B(\alpha, \beta) = \dfrac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} $$

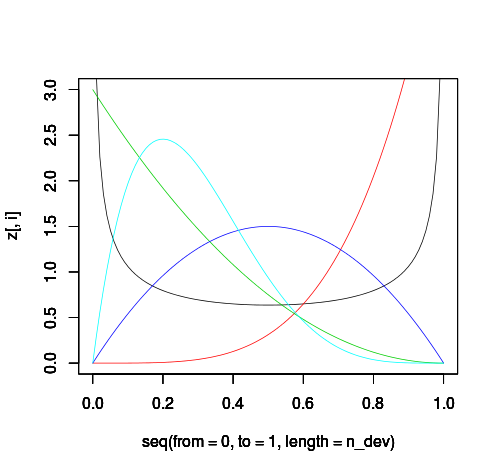
wikipediaと同じ図を描いてみる

• R

library("rgl")

#グラフは折れ線グラフで近似する。分割の個数。
n_dev = 100

alpha <- c(0.5, 5, 1, 2, 2)
beta <- c(0.5, 1, 3, 2, 5)
f <- function(a, b) dbeta(seq(from=0, to=1, length=n_dev), a, b)
z <- mapply(f, alpha, beta)

#グラフを重ねるのにpar(new=T)を使う
for (i in 1:5){
  plot(seq(from=0, to=1, length=n_dev) , z[,i], xlim=c(0,1), ylim=c(0,3), col=i, type='l')
  par(new=T)
}

Rはimport文を書かなくても結構使えるのでさくっと計算するときにも便利である。

• python

from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt

#n_devは100だとa=b=0.5のときにx=0,1付近で無限大になるのが余り分かりやすくなかった
n_dev = 1000
a = (0.5, 5, 1, 2, 2)
b = (0.5, 1, 3, 2, 5)

#beta.pdf(x, alpha, beta)を使う
x = np.linspace(0, 1, num=n_dev)
f = lambda a, b: beta.pdf(x, a, b)
y = np.array([beta.pdf(x, a, b) for a, b in zip(a, b)])

for i in range(5):
    plt.plot(x, y[i])

plt.show()

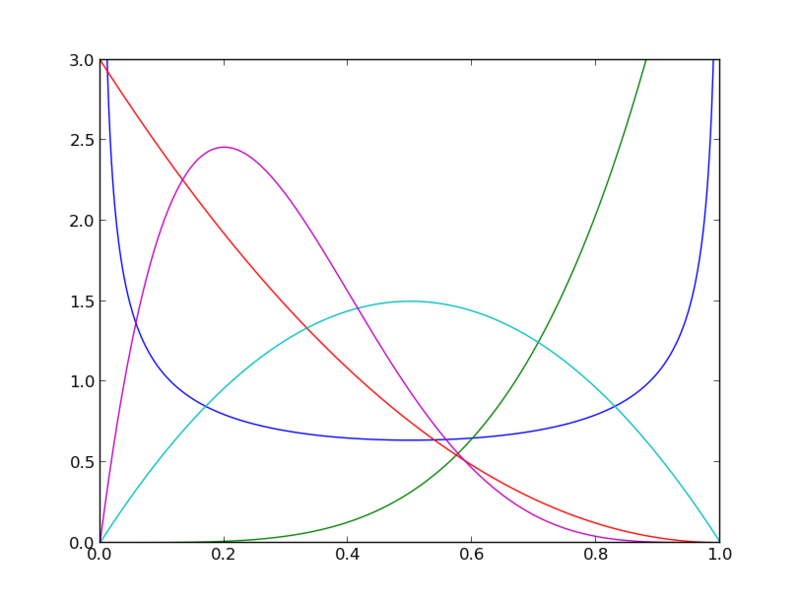
pdfなのでこれ単体で意味を持つわけではないが、例えば尤度を計算するときにはpmfをビンごとに積分して求める、あるいは一次近似で良いならpdfをそのまま使って後で正規化することもできる。