この記事には数式の間違いがあるので注意
その1、その2の続き。前回は母集団の推定分布$\hat{F_{K}}$に対して$F_{K}$がどのくらいの位置にいるかを調べた。今回はこの値(p)が、母集団がどのような分布のときにどれくらい誤差を生じるのかを調べたい。
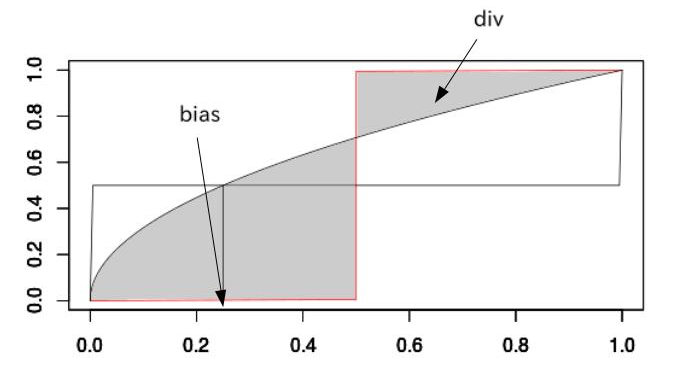
pが上の曲線のように分布している時に、pの中央値と0.5の差をbias、斜線部分の面積をdivとする。理想的な分布の時biasは0になることが予想される。divは扱いがわからないのでひとまずプロットしてみる。
このプログラムは計算のロスが大きい雑なコードなことに注意。
from __future__ import division import numpy as np from scipy.special import gammaln, gamma from scipy.stats import beta import matplotlib.pyplot as plt import matplotlib as mpl import matplotlib.patches as patches from matplotlib.path import Path # 予測分布での母集団が位置するcdf、予測分布の広さの計算(ppf) def calc_p(Us, Fs_ori, Ks): Q = Us.sum() a = Us + 1 b = Q - Us + np.array(Ks, ndmin=2).T - 1 cdf = beta.cdf(Fs_ori, a, b) cdf[np.isnan(cdf)] = 0 ppf0 = beta.ppf(0.05, a, b) ppf0[np.isnan(ppf0)] = 0 ppf1 = beta.ppf(0.95, a, b) ppf1[np.isnan(ppf1)] = 0 ppf = ppf1 - ppf0 lpmf_Ks = gammaln(Q + Ks) - gammaln(2 * Q + Ks) - (gammaln(Q + Ks[0]) - gammaln(2 * Q + Ks[0])) pmf_Ks = np.exp(lpmf_Ks) #normalize return (cdf.T * pmf_Ks).sum(axis=1) / pmf_Ks.sum(), (ppf.T * pmf_Ks).sum(axis=1) / pmf_Ks.sum() # biasとdivの計算 def stat_p(arr): bias = np.median(arr, axis=0) - 0.5 div = np.empty([arr.shape[1]]) for i in range(arr.shape[1]): tmp = arr[:, i] div[i] = (tmp[tmp > 0.5] - 0.5).sum() + (0.5 - tmp[tmp <= 0.5]).sum() div /= arr.shape[0] return bias, div prec = 20 Bias = np.zeros([prec, prec]) DivP = np.zeros([prec, prec]) DiffP = np.zeros([prec, prec]) for i in range(1, prec): for j in range(1, prec - i): K_ori = len(Fs_ori) Fs_ori = np.array([i / prec, j / prec, 1 - i / prec - j / prec]) # n_sample = 1000 Us = np.random.multinomial(n_sample, Fs_ori) # K_sup = 5000 Ks = np.arange(K_ori, K_sup) n_sim = 10#000 p = np.empty([n_sim, K_ori]) diff = np.empty([n_sim, K_ori]) for k in range(n_sim): p[k], diff[k] = calc_p(Us, Fs_ori, Ks) # 処理を細かく書くのがしんどかったので手抜き。計算結果を1つだけとって後は捨てる bias, div = stat_p(p) Bias[i - 1, j - 1] = bias[0] DivP[i - 1, j - 1] = div[0] # 3種類全部帰ってきたもの全ての平均になっていたので訂正 # diff.shape = (4997, 3) # 訂正前 # DiffP[i - 1, j - 1] = diff.mean() # 訂正後 DiffP[i - 1, j - 1] = diff[1].mean() #--------------- # プロット #--------------- def plotframe(): verts = [(0, 0), (1, 0), (0, 1), (0, 0)] codes = [Path.MOVETO, Path.LINETO, Path.LINETO, Path.CLOSEPOLY] path = Path(verts, codes) patch = patches.PathPatch(path, edgecolor='black', facecolor='none', linewidth=3) ax.add_patch(patch) def plotcontour(x, y, z, cmap): CS = ax.contourf(x, y, z, 20, cmap=cmap) #contour line CS1 = ax.contour(CS, levels=CS.levels[::4], colors='black') #label the contour ax.clabel(CS1, inline=1, fontsize=8) # colormap colors = [(1, 1, 1)] colors.extend(mpl.cm.autumn_r(np.linspace(0, 1, 10))) cmap = mpl.colors.ListedColormap(colors) x = y = np.linspace(0, 1, prec) ax = plt.subplot(311) plotcontour(x, y, DivP, cmap) ax.set_title("DivP") plotframe() ax = plt.subplot(312) plotcontour(x, y, Bias, cmap) ax.set_title("Bias") plotframe() ax = plt.subplot(313) plotcontour(x, y, DiffP, cmap) ax.set_title("DiffP") plotframe() #%matplotlib inline #plt.rcParams['figure.figsize'] = 20, 20 plt.show()
訂正前
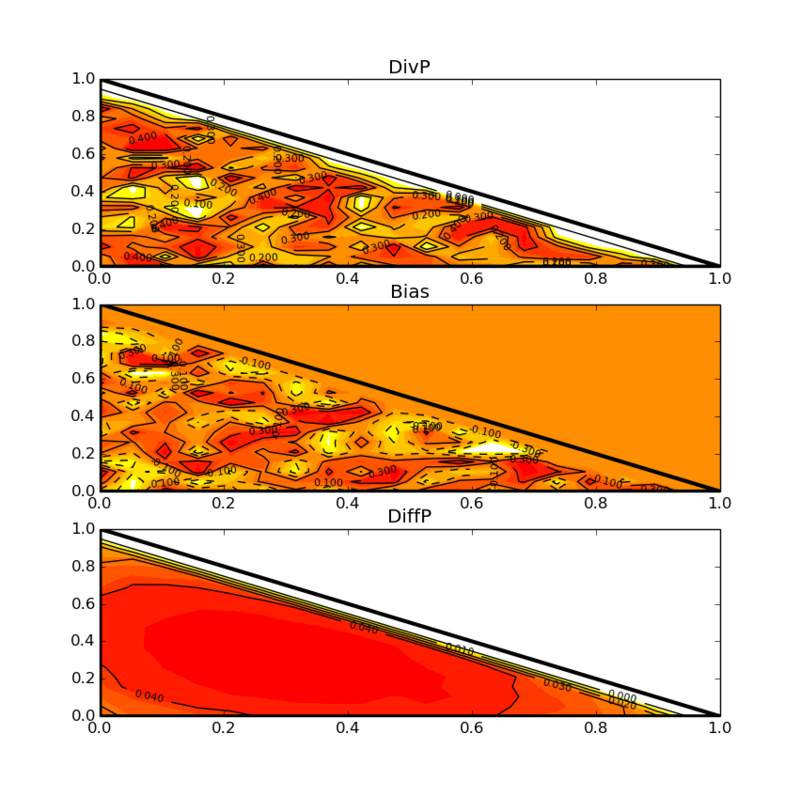
訂正後
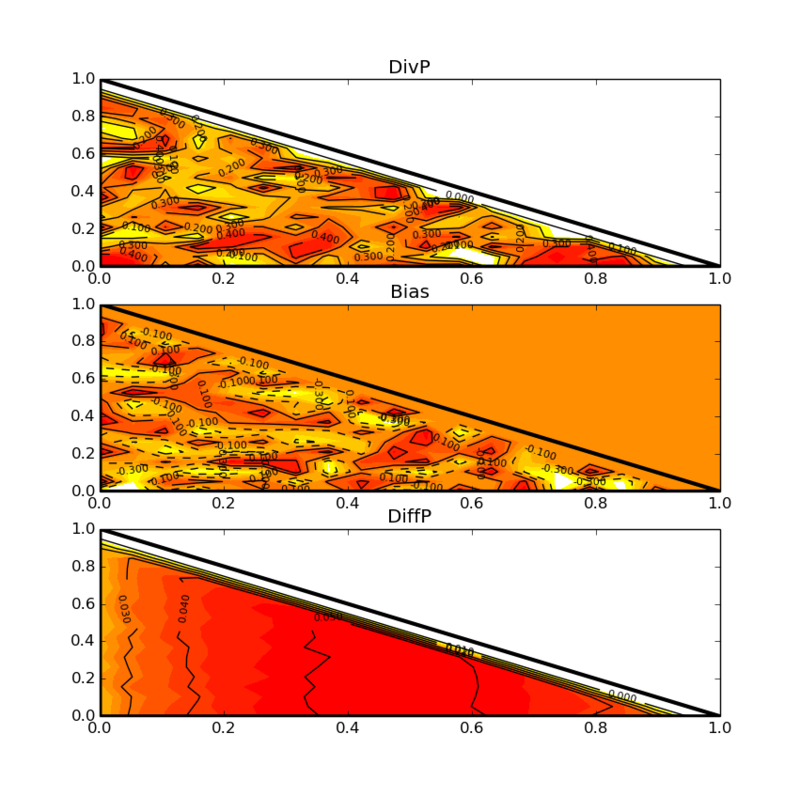
なにやらグチャグチャした分布が現れた。繰り返し計算させる必要があるがpythonではちょっと遅すぎる。