復習。2章は短い。関数宣言、リスト、タプル、リスト内包について。
基本的な演算子
- 四則演算:
+、-、*、/はpython3と同じ。破壊的代入はできないので+=などは使えない。 - 商、余り
> div 3 2 1 > mod 4 2 0
- 論理演算:
> True && False -- and True > True || False -- or False > 4 /= 3 -- 等しくない True
==、not Trueとかも使える。
Calling Funtions
その他
- succは引数の型に属する次の値を返す。(例:succ 1 == 2、succ 'a' == 'b')
- StringとCharは区別する。
文字列(string)は"で囲み、一文字(Char)は'で囲むことで区別する。 - min、maxは2つの数の最小、最大
- 引数を2つ取る関数は
min 2 3という表現だけでなく2 `min` 3とも書ける。
Baby's First Functions
関数宣言
関数は
doubleMe :: Int -> doubleMe x = x + x
のように宣言する(詳しくは第3章)。
この関数を使って、
doubleUs x y = double x + double y
のように新しく関数を作れる。
IF文(式)
関数型言語はプログラムを関数で記述していく。条件分岐は必要なのでHaskellにもif構文は存在するが、通常の手続き型言語と違ってif構文も関数なので、値を返す必要がある。そのためにif構文には必ずelse句がある。
myfizz x =
if div x 15 == 0
then "fizzbuzz"
else if div x 3 == 0
then "fizz"
else if div x 5 == 0
then "buzz"
else show x
などと標記する。実際にはガード構文のほうがこのような例ではすっきりする。
ifも関数なのでfunc x = (if x>0 then "+" else "- or 0") ++ "dayo"みたいに値として扱うこともできる。
インタプリタ特有の注意
- インタプリタ上での変数aの宣言は
> let a = value
とする。
;で区切ればGHCi中でも宣言するのに複数必要な関数なども宣言できる。
> let addThree :: Int -> Int -> Int -> Int; addThree x y z = x + y + z
An Intro to Lists
リストについて注意
- その1: ハスケルでは文字列もリストと同じ扱いになっていて、Charのリストであることに注意しておく。つまり、
['c', 'e'] ++ ['l', 'l'] == "cell"であること。
- その2: 型について。[, ]と[[]]は同じ型である。
- その3: リストには同じ型の要素しか入れられない。
- リストの連結:
++ - リストの先頭へ要素を追加:
:(例: [0, 1, 2, 3] == 0:[1, 2, 3] == 0:1:[2, 3]) - リストの要素へのアクセス(インデックスは1から):
!!(例:[1,2,3] !! 2) - リストの比較:
>、>=、==など。リストの先頭から順に要素を取り出して比較する。要素がなくなったら終わり。(例: [1, 2] < [3]) - リストから..:
head、init、last、tail
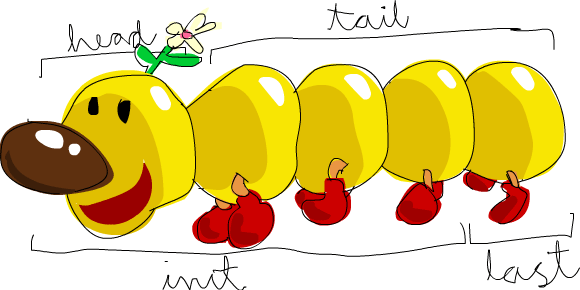
(learnyouahaskell.comより)
もちろん空のリストを渡したりするとエラーが出る。
- length:
length [1,2,3]とする。pythonじゃないしobject.lengthみたいな感じではない。(pythonでもlen(List)だけど) - null:
null [1,2,3]--> Falseみたいなすごいやつ - reverse:
reverse [1,2,3] - take: 一つ目の変数に数、2つ目にリストをとって数の分返してくれる。
take 4 "unkou"
- drop: 指定された数だけ要素を削除する。
drop 1 [1]-->[] - maximum, minimum: max, minが引数を二つ取る関数だったのに対し、こちらはリストを引数に取る関数。
- product:
product [1, 2, 3]--> 6 - sum: 普通のsum
- elem:
elem 'a' "apple"--> True - cycle: 与えられた要素の無限リストを返す。
cycle [1, 2]-->[1, 2, 1, 2, 1, 2, .. - replicate:
"mega" ++ replicate 2 "mawaru" ++ "yo"-->"megamawarumawaruyo"
Texas Ranges
入力を怠ける方法。
[1..2*5] --> [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]、[1..]、['a'..'g'] --> "abcdefg"等で使える。
それほど賢くないので等差数列が限界。小数も精度が悪いのでやめたほうがいい。
I'm a List Comprehension
普通の集合みたく、{ \(f(a) | a \in \mathbb{R} \) }というふうに表記する。
> let seito = ["majime", "majime", "noukin", "baka", "majime", "ryunen"] > [if elem x ["noukin", "baka"] then "doryokujin" else x| x <- seito, x /= "ryunen"] ["majime", "majime", "doryokujin", "doryokujin", "majime"]
いいクラスになった。
length' xs = sum [1 | _ <- xs]
とかもできる。_は名無し変数みたいなもので捨てられるためだけに使われている。
Tuples
タプルはリストと違って違う型を入れることができることと、要素の数によって型が違うことがポイント。専用の型定義がどこかに有りそうだけどベクトルとかに使えば便利そう。
- fst, snd: 2つ要素を持つタプルのそれぞれ1つ目、2つ目の要素を返す。
- zip: リストを2つ取って、タプルの組にして返す。
> zip [1,2,3] "abc" [(1, 'a'), (2, 'b'), (3, 'b')] > zip [1..] ["go", "e"] [(1, "go"), (2, "e")] --「一期一会」にはならない(笑)