tak0kadaの何でもノート

発声練習、生存確認用。

医学関連は 医学ノート へ

超古典的な数値積分手法

数学 数値積分

いくつか調べた中で区間を等間隔して積分するという最も単純なものを列挙する。

以下$\int f dx$を積分する場合を例とする

公式

  • 長方形近似
    • $\sum \Delta x f(x_{i})$
  • 台形近似
    • $\sum \Delta x (f_{i}/2 + f_{2} + \cdots + f_{n-1} + f_{n}/2)$
    • 2 台形公式: 台形近似はテイラー展開すると2次まで一致することが分かる
  • simpsonの公式(2次関数近似)
    • $\sum \dfrac{\Delta x}{3}(f_{1} + 4f_{2} + 2f_{3} + 4f_{4} +\cdots+ f_{n})$
  • newtonの公式(3次関数近似)
    • $\sum \dfrac{3\Delta x}{8}(f_{1} + 3f_{2} + 3f_{3} + 2f_{4} + 3f_{5} +\cdots+ f_{n})$
  • 4次関数近似
    • $\sum \dfrac{2\Delta x}{45}(7f_{1} + 32f_{2} + 12f_{3} + 32f_{4} + 14f_{5} + 32f_{6} +\cdots)$: この後どう続くか不明
  • Romberg積分

練習

  • $\int_{0}^{1} \frac{4}{1+x^{2}}dx = \pi$
from numpy import pi
import matplotlib.pyplot as plt

def f(x):
    return 4/(1 + x**2)

def simpson(n_div):
    n = n_div
    nu = 0
    for i in range(n):
        if i == 0 or i == n - 1:
            nu += f( i / (n - 1) )
        elif i % 2 == 0:
            nu += 4 * f( i / (n - 1) )
        else:
            nu += 2 * f( i / (n - 1) )
    return nu / 3 / (n - 1)

plt.plot([simpson(100 * i) for i in range(1, 100)])
plt.axhline(y=pi, color='r')
plt.show()

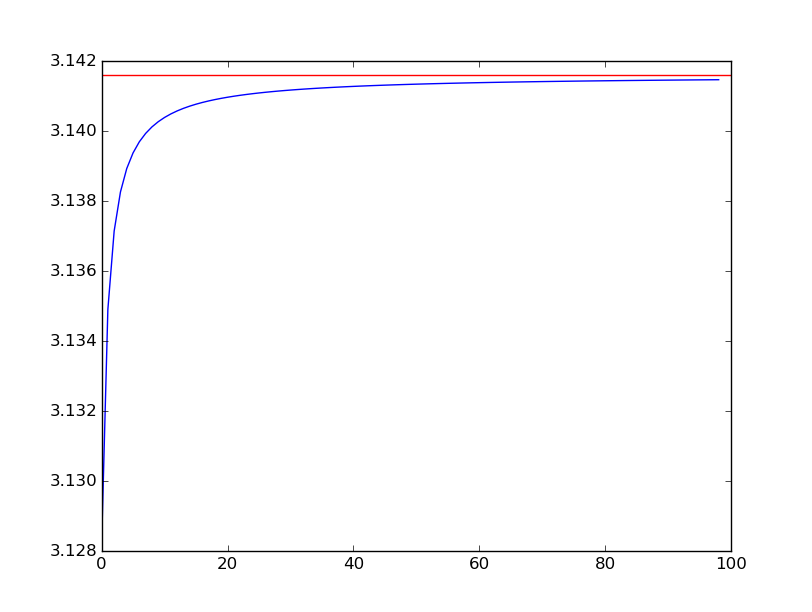
  • $\int_{0}^{1}dr \int_{0}^{\pi}d\theta \int_{0}^{2\pi}d\phi r^{2}\sin{\theta} = \frac{4\pi}{3}$
import numpy as np
import matplotlib.pyplot as plt

def f(r, u, v):
    return r ** 2 * np.sin(u)

def rect(n):
    ret = 0
    dv = np.pi * 2 * np.pi / ((n - 1) ** 3)
    for ri in range(n):
        r = ri / (n - 1)
        for ui in range(n):
            u = np.pi * ui / (n - 1)
            for vi in range(n):
                v = 2 * np.pi * vi / (n - 1)
                ret += r ** 2 * np.sin(u) * dv
    return ret

def simpson_1(n, a, b, f):
    ret = 0
    for i in range(n):
        if i == 0 or i == n - 1:
            ret += f(a + (b - a) / (n - 1) * i)
        elif i % 2 == 0:
            ret += 4 * f(a + (b - a) / (n - 1) * i)
        else:
            ret += 2 * f(a + (b - a) / (n - 1) * i)
    return ret / 3

def simpson(n):
    dv = np.pi * 2 * np.pi / ((n - 1) ** 3)
    return dv * \
    simpson_1( n, 0, 1, lambda r: \
        simpson_1( n, 0, np.pi, lambda u: \
            simpson_1( n, 0, 2 * np.pi, lambda v: f(r, u, v) )
        )
    )

plt.plot([rect(15 * i) for i in range(1, 10)], color='b')
plt.plot([simpson(15 * i) for i in range(1, 10)] , color='g')
plt.axhline(y=4/3*np.pi, color='r')
plt.show()

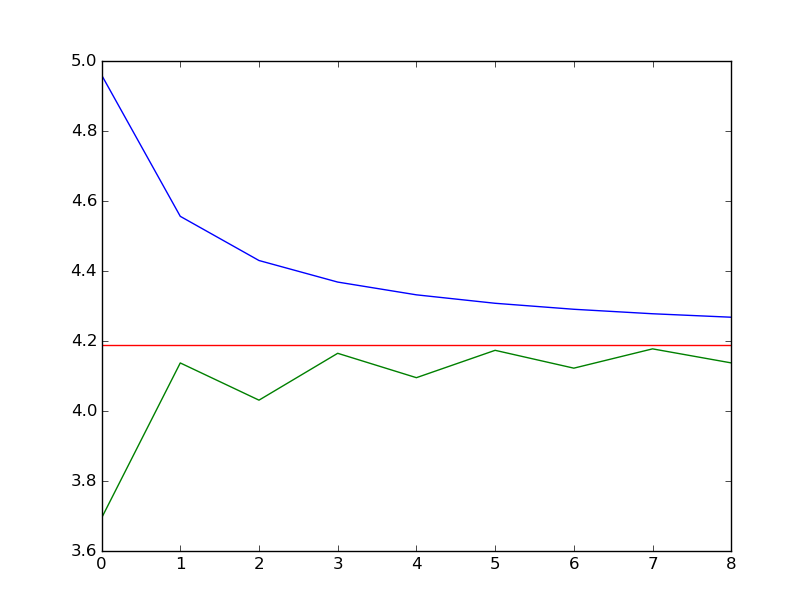
ラムダ式をうまく使って綺麗にかけたので満足。