細胞の形の分析に取り組んでいるわけだが、バイオリンの形に関する分析の論文があったので読んでみた。以下は手法と解釈についてのメモ。数学的に厳密な理解までは手が届いていない。
- 変数として、楽器の種類、作者、製造年、土地、形を考えてそれらの関係を調べる。
- 形は楕円フーリエ記述子解析、調和関数を基底として展開する。
- 「形」はそのままだと扱えないので、数学の助けを借りないなら面積などでクラス分けしてカテゴリ変数にすることになりそう。(少し恣意的か?)
- バイオリンの画像は上から撮った写真を二値化したものを用いる。競売のためのもので、高級なものが多いなどの選択バイアスがありそう。
形が連続で高次元ということで、一番情報量が多いからか、形を説明変数に用いている。
解析手法
- 主成分分析でまとまった指標を作る
- 線形判別解析でクラス分けする
- 階層クラスタリングで系統の有無を調べる
主成分分析と線形判別解析の共通点としては、ひとまとまりにすることで次元を削減する点がある。違いとしては
- 主成分分析は全体を説明する←→線形判別解析は集団内での違いを説明する
- 主成分分析: 固有ベクトルの係数のベクトルという連続な指標になる←→線形判別解析: 順序のつかないカテゴリ指標にクラス分けする
1. 主成分分析(PCA)
楕円フーリエ記述子解析
- ここでは楕円フーリエ記述子解析で取り出したベクトルを主成分分析する
- 楕円フーリエ解析参考サイト1、参考サイト2
- これは中村さんが自己紹介の時に説明していた解析とおそらく同じ
- 楕円は3パラメータで決定される
- MΦの形など角度から円弧へ一対一の対応がない場合は事前に変形が必要
- 他にも基底はありえるらしい。無限次元なら自由だと思うが離散なら基底次第で取れる情報が変わりそう
主成分分析
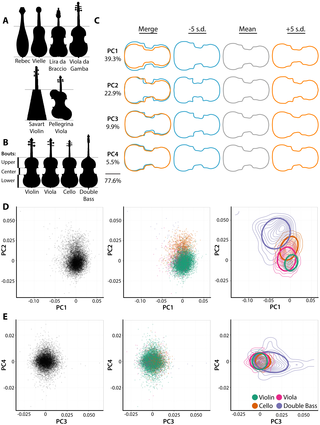
- 「主な」方向から順に取り出していく
- 一般的に固有ベクトルはPC1、PC2と命名される
- 主な成分から取り出すのですべての基底をとり出さなくても全体の説明がつく(次元削減)
- Dの図を見るとPC1軸の方がPC2軸より分散が少ないのは取り出す順番のため
2. 線形判別解析(LDA)
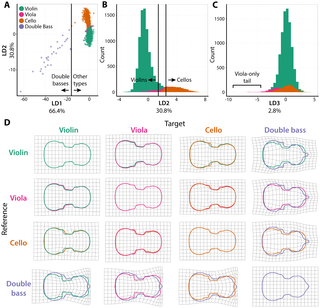
調和関数
- PCA参考サイト2に出てくるL.Shenさんの論文でも見られる
- 線形判別解析の方が細かい解析をしやすいのでMANOVA、スピアマンの順序相関係数が使われている
- ここでは調和関数を基底として展開する
MANOVA
スピアマンの順序相関係数

- スピアマンの順位相関係数
- 順序のある2つの変数の差を図る方法。順番のみに依存するノンパラメトリック手法。-1が逆向き、1が順方向の相関、0が無相関を表す
- Bのグラフはρ値の絶対値が小さいなら帰無仮説が否定されるということがわかる
3. 階層クラスタリング
階層化クラスタリングは系統の分岐を調べてグループごとに解釈をするのに役立つ。
4. その他、可視化
Thin Plateスプライン

- Dの網目はThin Plateスプラインのプロット
- 形の変化を目で見やすい(3次元以上は苦しそう)
ボックスプロットその他
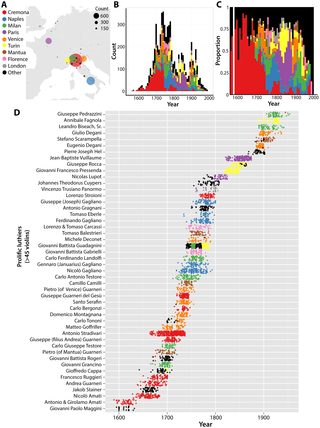
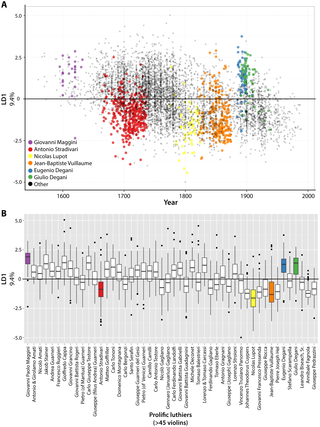
ボックスプロットを複数並べるだけでも結構な情報量がある。