PLOS Biology: The Extent and Consequences of P-Hacking in Scienceを読んだ。
世の中にはp値が小さい(つまり統計的に有意)なデータが尊ばれる傾向がある。そうすると発表される結果は有意なものばかりだし、悪ければ詐称かもしれない。間違った結果を集めてしまうとメタ解析してもバイアスが残る。そこでp-hackの可能性を検定する方法を扱った論文。
のはずなんだけど、知識がないからか「本当にこれでいい」のかという疑問が残った。以下概要。
1. p-hackingとは?
研究者がやりがちなバイアスとしてselection bias、inflation biasがある。selection biasは有意でない実験結果が世に出ないこと。inflation biasはいわゆるp-hackingで、「効果量」が小さいのにサンプルサイズを大きくしたり、都合の良い検定手法で発表してしまったりすること。
2. 考え方
p値ハッキングを見抜けないとメタ解析もバイアスを受けるのでその方法としてp値の分布(p-curve)を使おう、というのがこの論文の提案。以下ではp値が<0.05で有意とする場合について考える。
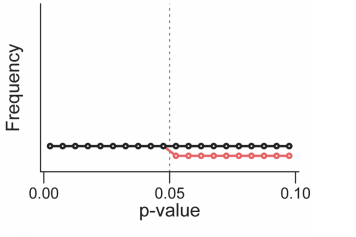
効果量が0な実験からのp値は一様分布になる。ここにselection biasがかかるとp>0.05でグラフが不連続に低下する。
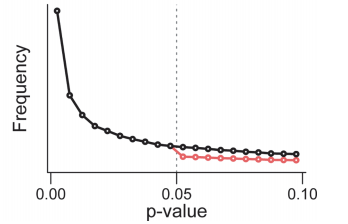
効果量が0でない実験からは小さいp値が出る確率が高いのでp-curveは右下がりになる。selection biasがかかるとp>0.05でグラフが不連続に低下する。
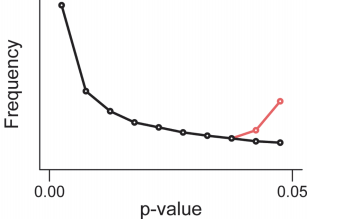
p値ハッキングではp>0.05なのを無理やり0.05を下回らせる作業をするので、0.05の左側で不自然な右上がりが現れる。
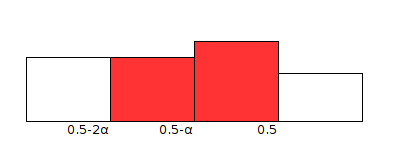
p-hackingをするとぎりぎり0.5を下回らないp値を無理やり小さくするので、「0.5-2α<p<0.5-α」に入るp値が「0.5-α<p<0.5」に入るp値よりも少なくなる。そこで帰無仮説を「p値がそれぞれのビンに入る確率は0.5」として、データより偏った結果が出る確率が閾値より小さければ、帰無仮説を棄却する。(片側2項検定)
例えば26個のp値があって、10が「0.5-α<p<0.5」、16が「0.5-2α<p<0.5-α」に入った時、
> sum(dbinom(x = 0:10,size = 26,prob = 0.5))
0.1634698
> binom.test(c(10,16),alternative = "less")
Exact binomial test
data: c(10, 16)
number of successes = 10, number of trials = 26,
p-value = 0.1635
alternative hypothesis: true probability of success is less than 0.5
95 percent confidence interval:
0.0000000 0.5643373
sample estimates:
probability of success
0.3846154
感想
上の方法を使って怪しい結果を消すことで「正しい」結果が得られるとのことだった。この手法で自分が違和感を感じているのは以下のようなケース。
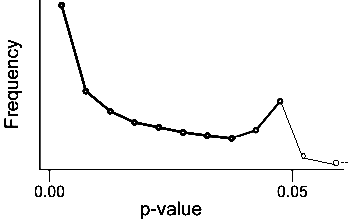
0.05より大きいところにはもともとp値があまりない場合でp-hackが見られるようなとき(不正する意味ないか...)、つまりp値の平均が0.05より小さい時に、0.05周辺のデータを無視すると有意な結果ばかり抜き出した解析にならないのかということが気になっている。メタ解析の仕方とか効果量の勉強をすれば理解できるのかな...?