リサンプリング法
母集団から何度も標本抽出して調べられるのは理想であるが、実際には不可能なことが多い。しかし、得られている推定量\(\hat{\theta}\)の性能を把握するために\(\hat{\theta}\)の分布を知りたい。このような場合に、ランダムなリサンプリング(モンテカルロ法)によって求めた統計量の分布からパラメータの確率分布や誤差を推定することを考える。解析的な方法ではないので、変数の分布についての情報がない状態でも分布をヒストグラムとして得ることができる。(参考: 三中先生のスライド)
- ノンパラメトリック・ブートストラップ法: 分布の形式を仮定しない
- パラメトリック・ブートストラップ法: 分布の形式を仮定する
1. ブートストラップ法
重複を許して無作為同数リサンプリングを繰り返す。
1.1 信頼区間
scikits.bootstrapをインストールする
sudo easy_install scikits.bootstrap
男性の身長でやってみる。*1
import numpy as np from scikits import bootstrap men_heights = np.random.normal(loc=170, scale=5.5, size=(100,)) print(bootstrap.ci(men_heights, alpha=0.05, method='bca'))
差の検定
男性と女性の差を調べる
1.2.1 テキストに乗っていた手順で調べる
男女の平均が異ならない(同じ)だという帰無仮説に基づいて考え、この仮説のp値を求める。男女の差はないはずなので一緒にまとめた集団を作り、その集団から標本に現れた差が生じる確率をブートストラップで調べる。(片側検定)
from __future__ import division import numpy as np import matplotlib.pylab as pylab #日本人の男女の身長を大体正規分布と仮定する men_heights = np.random.normal(loc=170, scale=5.5, size=(100,)) women_heights = np.random.normal(loc=160, scale=5, size=(20,)) df = men_heights.mean() - women_heights.mean() heights = np.hstack((men_heights, women_heights)) times = 1000 n_boot = 1000 #heightsをソートしたものの3次元行列、以下ベクトル化して計算していく data = heights[np.random.randint(120, size=(120, n_boot, times))] #リサンプリングして平均を計算 diff = data[:100].mean(axis=0) - data[100:].mean(axis=0) index = diff > df # result = index.sum(axis=0)/times #プロット(男子と女子の平均身長の差が大きすぎてまともなグラフは描けないが) pylab.plot(np.sort(result)) pylab.show()
直感と同じく、男子の集団と女子の集団に現れた身長の差が偶然に生じることはほぼありえない(100000に1もない)ことが分かる。 *2
1.2.2 t検定
ブートストラップ法入門 - 千葉大学数学・情報数理学科では2群の差を検定統計量tを用いて調べている。(wikipediaによると、正規性検定してからt検定(Welchの検定)*3を行うらしいが特に言及されていない。)
定義
\[ \begin{align} t &\equiv &\mbox{平均の差}/\mbox{分散の推定値}\\ &= &\dfrac{|\bar{X}-\bar{Y}|}{σ}\\ &= &\dfrac{|\bar{X}-\bar{Y}|}{\displaystyle \sqrt{\hat{σ}_{x}^{2}/(m -1)+\hat{σ}_{y}^{2}/(n-1)}} \end{align} \]
帰無仮説を満たす母集団から標本抽出をするので \[ \begin{align} x_{i}' &= &x_{i} - \bar{x} + \bar{z}\\ y_{i}' &= &y_{i} - \bar{y} + \bar{z} \end{align} \]
ブートストラップ推定値も差し込みの原理から同様にして計算する。 \[ t^{\ast} = \dfrac{(X^{\ast} - Y^{\ast})}{\displaystyle \sqrt{S_{x}^{\ast 2}/(m -1) + S_{y}^{\ast 2}/(n -1)}} \]
やってみる
from __future__ import division import numpy as np import matplotlib.pylab as pylab n_boot = 200 times = 100 x = np.random.normal(loc=170, scale=5.5, size=(100,)) #height_men y = np.random.normal(loc=160, scale=5, size=(20,)) #height_women xy = np.hstack((x, y)) data = xy[np.random.randint(120, size=(120, n_boot, times))] #xとyをリサンプリングしたものの平均 x_ = data[100:].mean(axis=0) y_ = data[:100].mean(axis=0) #z_ = data.mean(axis=0) #分散 Sx = dat[:100].var(axis=0) Sy = dat[100:].var(axis=0) #tのブートストラップ推定値 t_ast0 = np.abs(x_ - y_)/np.sqrt(Sx**2/(100-1)+Sy**2/(20-1)) t_ast = t_ast0.mean(axis=0) pylab.plot(np.sort(t_ast)) pylab.show() #観測されたxとyの値からt値を計算してブートストラップ推定量と比べる t = np.abs(x.mean() - y.mean())/np.sqrt(x.var()/(100-1) + y.var()/(20-1)) p = np.count_nonzero(t_ast > t) print("p="+str(p))
tが10くらいなのに対して\(t^{\ast}\)をソートして並べたものは
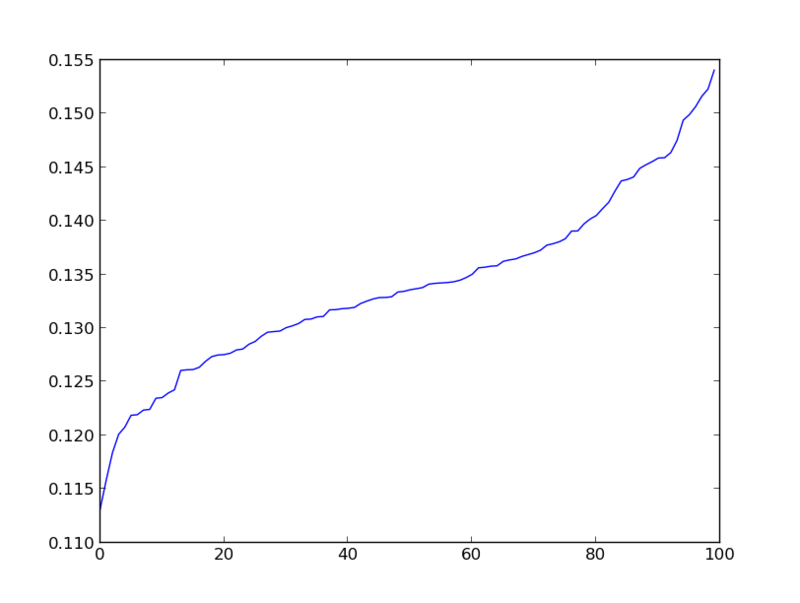
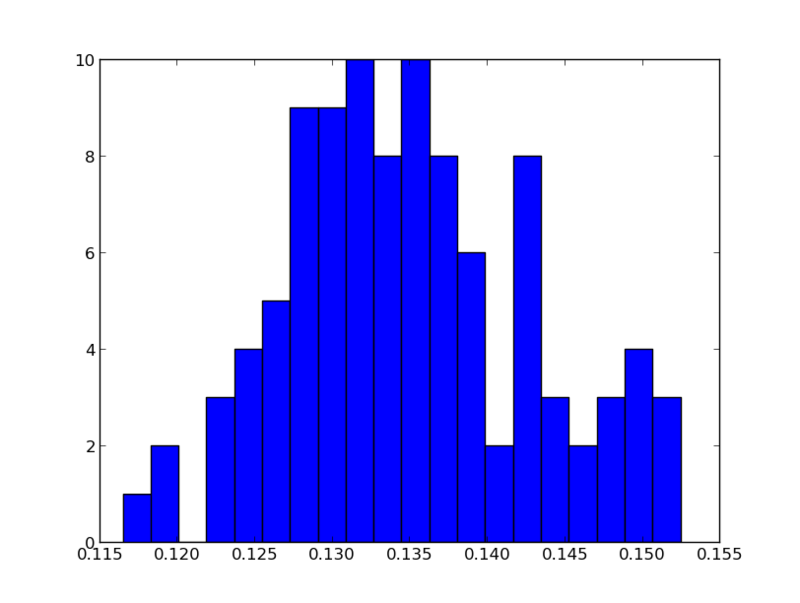
なので\(p=0\)になるのも当然であった。どちらの方法が一般的なのだろうか。
通常のt検定
from scipy import stats #equal_var=Trueで分散が等しい場合のt検定、FalseでWelchのt検定 t, p = stats.ttest_ind(x, y, equal_var=False) print("t-value = " + str(t)) print("p-value = " + str(p))
詳細
上の二つの例はよく見ると、一方の方法がBCaという方法でもう一方はただ単にパーセンタイル順位を調べただけのようである。実際、ブートストラップ法には種類が複数あって、
- 正規分布近似法: normal theory interval
- パーセンタイル法: percentile interval
- BCa法: Bias-Corrrctrd Accelerated Non-Parametic
- ABC法: Approcimate Bootstrap Confidence
などがある。(マルチスケール・ブートストラップ法というより精度の高い方法もあるらしい。少し幾何が分からないと統計手法の誤差(収束の良さ)はシミュレーションしてみる以外に求める方法はないのか..?)
参考
ブートストラップ法入門: すごく簡単な説明。バイアスを求めるところが理解できていない。
stats.stackexchange: Explaining to laypeople why bootstrapping works
scikit.bootstrapその1
scikit.bootstrapその2(元の実装)
2. ジャックナイフ法
重複を許さず無作為削除リサンプリングを繰り返す。ブートストラップ法より計算量が少ない。
詳細
ブートストラップ法入門 - 千葉大学数学・情報数理学科を丸パクリすると、\(\hat{\theta}\)の不偏推定量\(\widetilde{\theta}\)を
\[ b_{J} = (n-1)(n^{-1}\sum \hat{\theta_{-i}} - \hat{\theta}) \] \[ \widetilde{\theta} = \hat{\theta} - b_{J} \] (ここで、\(\theta_{-i}\)はi番目の要素を除いて推定した値である。)
とすると、\(\theta\)は-2次の誤差になるらしい。
3. パラメトリック・ブートストラップ法
TODO