numpy.randomにはたくさんの関数が用意されていて分布だけでもかなりの種類があるが、今回はそれ以外の関数について値を得たい場合について考える。
実装
cdf-1(random.random_sample())
とすればいい。
説明
簡単のため離散的に考える。pdfが与えられた時、いくつかのxについてのみ考える。pmfはpdfから
\[ \rm pm f = \rm pdf\Delta_{x} \] として計算できる。
ここで、\(\rm cmf = \rm cumsum(pm f)\)なので、幅1の直方体を用いて、pmfを面積に対応させて図示すると、
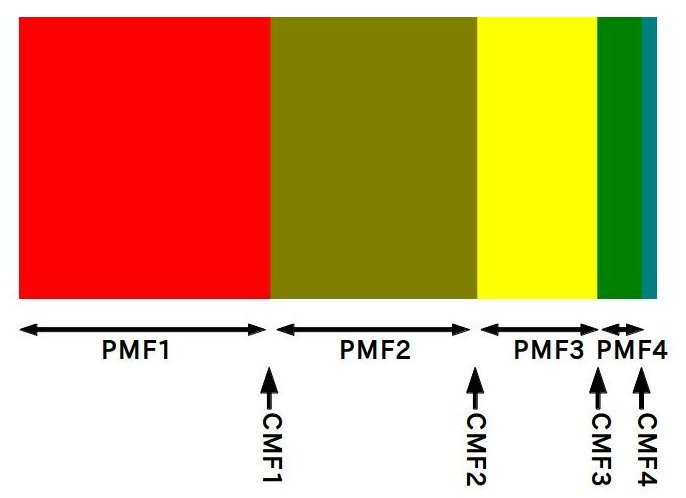
これから[0,1)の範囲で生成した乱数とcmfを比較すれば必要だったxが得られ、これを連続な場合に置き換えると、xはcdfの逆関数に対応していることが分かる。
直接は関係ないが高速な復元抽出の直感的な説明の説明のイラストがわかりやすかったので参考にした。